Skip to main content

Victoria Harbour, Hongkong

Github Repository

Dimensionality Reduction for Image Segmentation

Use Manifold Learning and the LD Analysis to Visualize Image Datasets.

Local Linear Embedding​

import matplotlib.pyplot as plt
import plotly.express as px
import pandas as pd
import seaborn as sns
from sklearn.datasets import load_digits
from sklearn.manifold import LocallyLinearEmbedding

Digits Dataset​

# load digits dataset with labels
X,y = load_digits(return_X_y=True)
X.shape
# (images, features)
# (1797, 64)
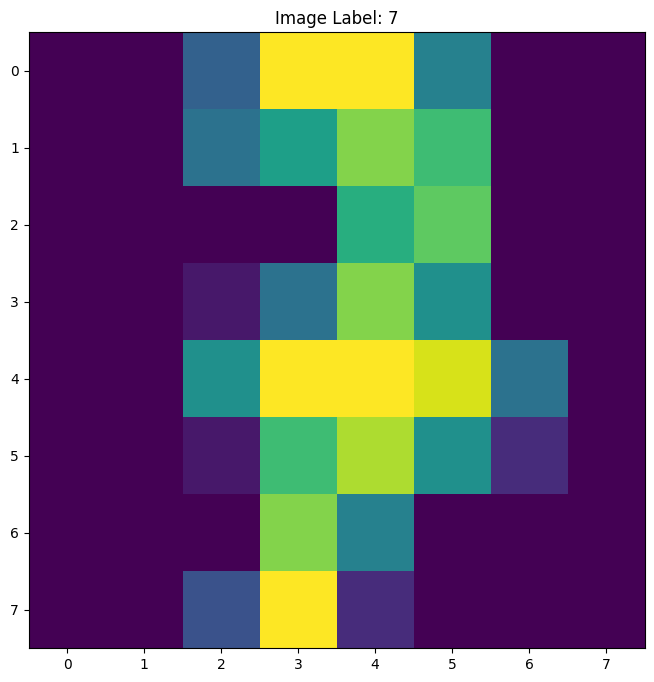
plt.figure(figsize=(8,8))
plt.title('Image Label: ' + str(y[888]))
plt.imshow(X[888].reshape(8,8))

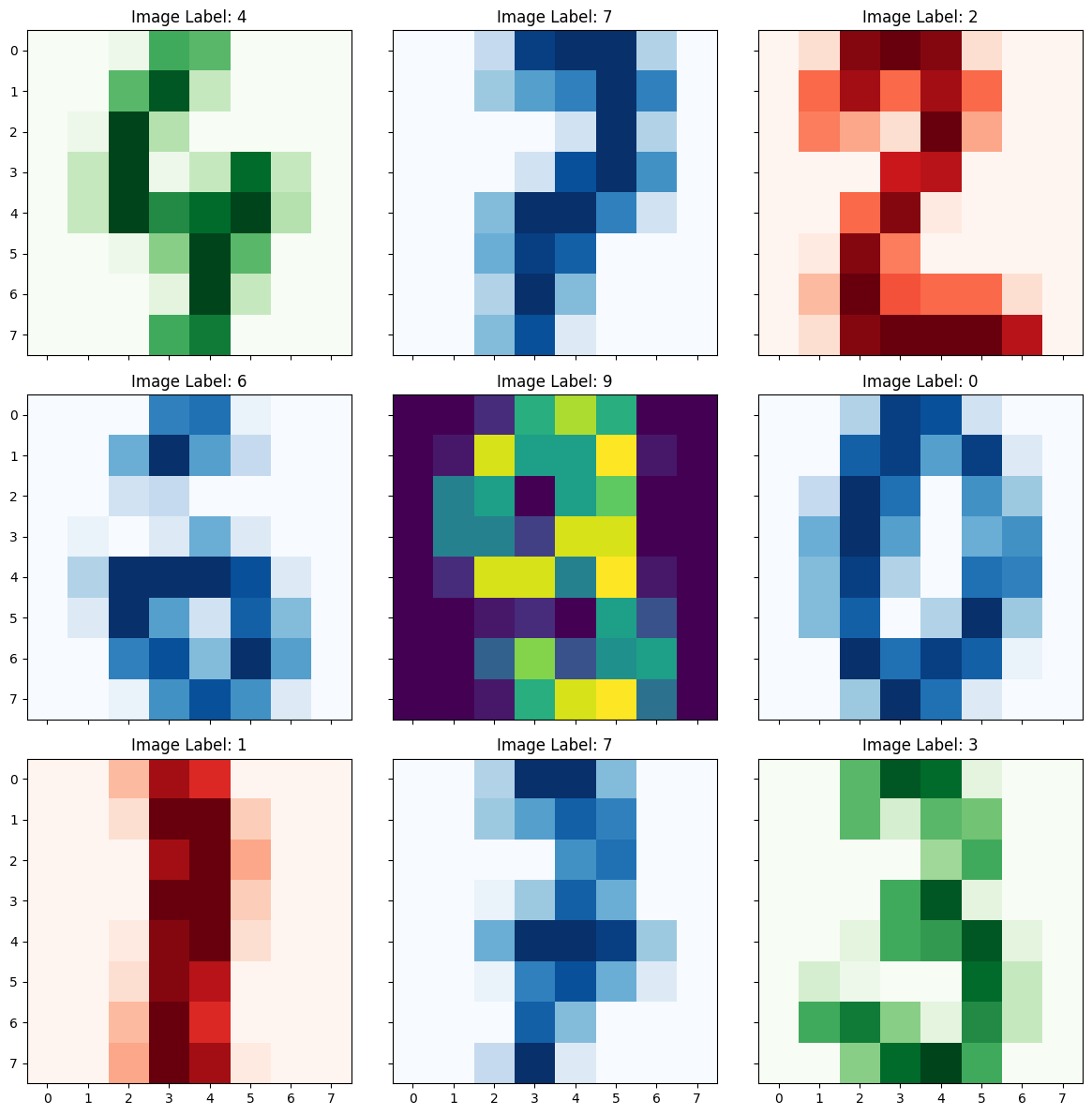
Dimensionality Reduction for Image Segmentation

fig, axes = plt.subplots(nrows=3, ncols=3, sharex=True, sharey=True, figsize=(12,12))
axes[0,0].title.set_text('Image Label: ' + str(y[111]))
axes[0,0].imshow(X[111].reshape(8,8), cmap='Greens')
axes[0,1].title.set_text('Image Label: ' + str(y[222]))
axes[0,1].imshow(X[222].reshape(8,8), cmap='Blues')
axes[0,2].title.set_text('Image Label: ' + str(y[333]))
axes[0,2].imshow(X[333].reshape(8,8), cmap='Reds')
axes[1,0].title.set_text('Image Label: ' + str(y[444]))
axes[1,0].imshow(X[444].reshape(8,8), cmap='Blues')
axes[1,1].title.set_text('Image Label: ' + str(y[555]))
axes[1,1].imshow(X[555].reshape(8,8))
axes[1,2].title.set_text('Image Label: ' + str(y[666]))
axes[1,2].imshow(X[666].reshape(8,8), cmap='Blues')
axes[2,0].title.set_text('Image Label: ' + str(y[777]))
axes[2,0].imshow(X[777].reshape(8,8), cmap='Reds')
axes[2,1].title.set_text('Image Label: ' + str(y[888]))
axes[2,1].imshow(X[888].reshape(8,8), cmap='Blues')
axes[2,2].title.set_text('Image Label: ' + str(y[999]))
axes[2,2].imshow(X[999].reshape(8,8), cmap='Greens')
plt.tight_layout()

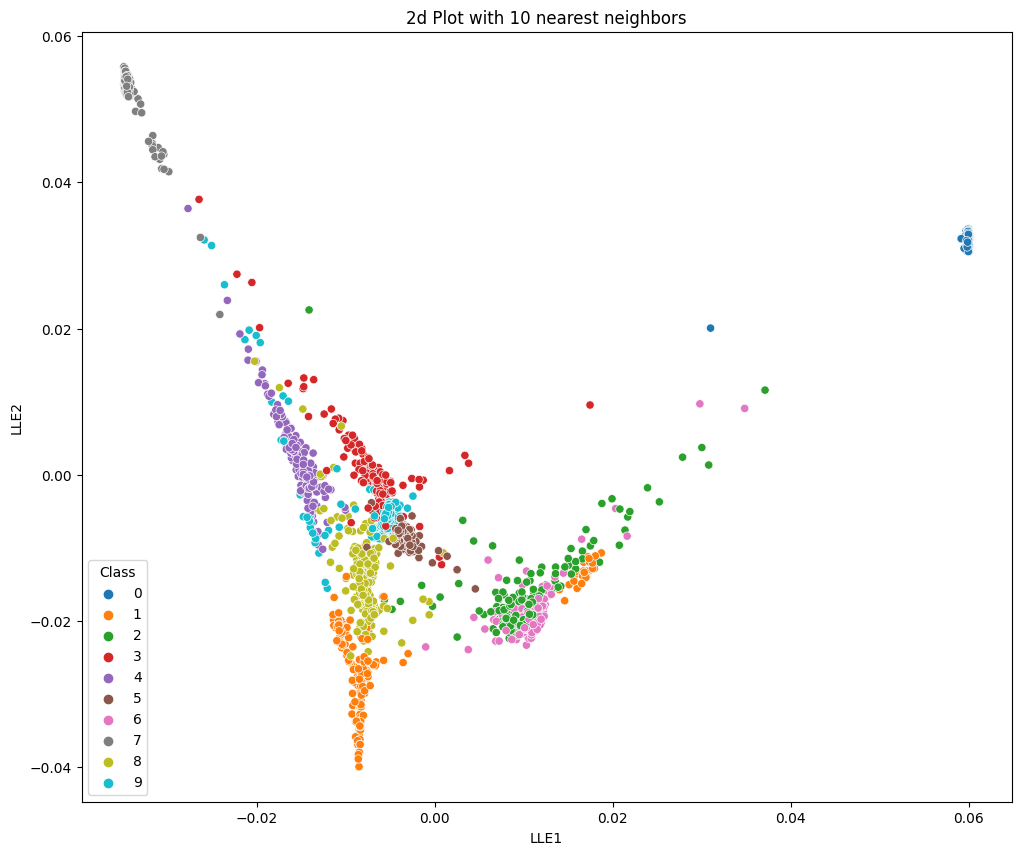
Dimensionality Reduction for Image Segmentation

2-Dimensional Plot​

# the dataset has 1797 images with 64 dimensions
# we use LLE to reduce the dimensionality of the dataset
# to help us visualize / classify it
no_components=2
no_neighbors=10

lle = LocallyLinearEmbedding(n_components=no_components, n_neighbors=no_neighbors)
X_lle = lle.fit_transform(X, y=y)

data = pd.DataFrame({'LLE1': X_lle[ :,0], 'LLE2': X_lle[ :,1], 'Class': y})

plt.figure(figsize=(12, 10))
plt.title('2d Plot with 10 nearest neighbors')
sns.scatterplot(x='LLE1', y='LLE2', hue='Class', data=data, palette='tab10')

Dimensionality Reduction for Image Segmentation

no_neighbors=15

lle = LocallyLinearEmbedding(n_components=no_components, n_neighbors=no_neighbors)
X_lle = lle.fit_transform(X, y=y)

data = pd.DataFrame({'LLE1': X_lle[ :,0], 'LLE2': X_lle[ :,1], 'Class': y})

plt.figure(figsize=(12, 10))
plt.title('2d Plot with 15 nearest neighbors')
sns.scatterplot(x='LLE1', y='LLE2', hue='Class', data=data, palette='tab10')

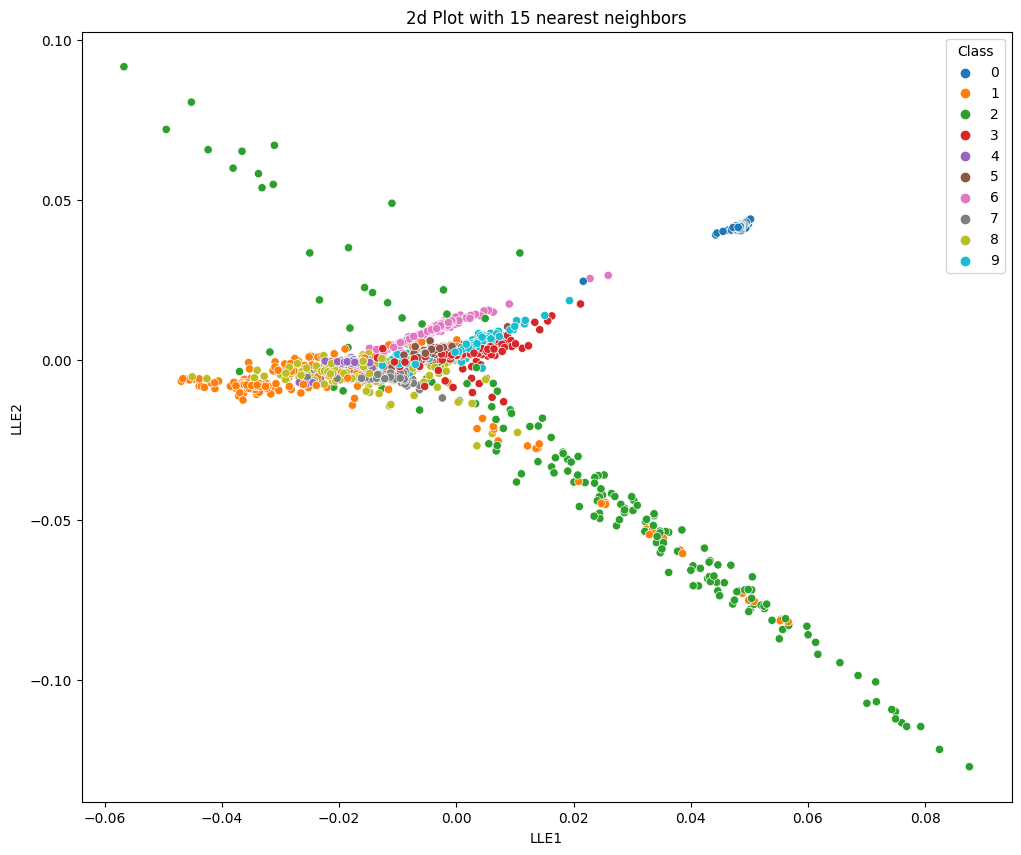
Dimensionality Reduction for Image Segmentation

no_neighbors=20

lle = LocallyLinearEmbedding(n_components=no_components, n_neighbors=no_neighbors)
X_lle = lle.fit_transform(X, y=y)

data = pd.DataFrame({'LLE1': X_lle[ :,0], 'LLE2': X_lle[ :,1], 'Class': y})

plt.figure(figsize=(12, 10))
plt.title('2d Plot with 20 nearest neighbors')
sns.scatterplot(x='LLE1', y='LLE2', hue='Class', data=data, palette='tab10')

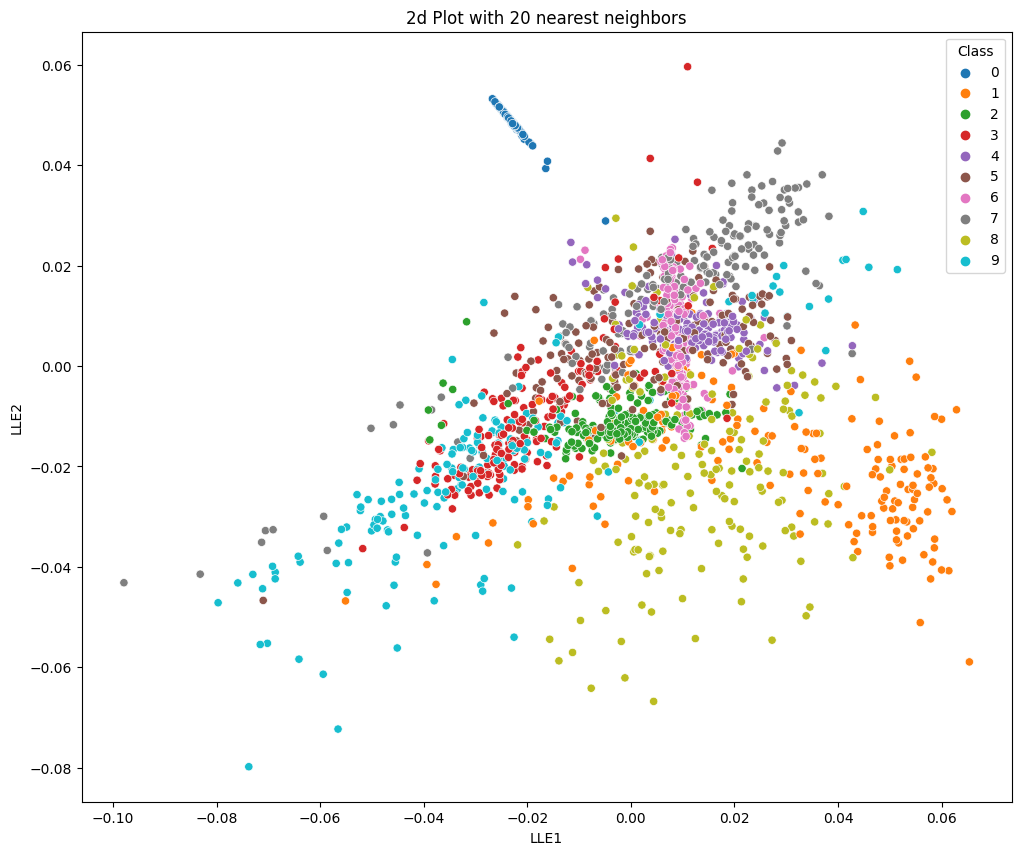
Dimensionality Reduction for Image Segmentation

3-Dimensional Plot​

no_components=3
no_neighbors=10

lle = LocallyLinearEmbedding(n_components=no_components, n_neighbors=no_neighbors)
X_lle = lle.fit_transform(X, y=y)

data = pd.DataFrame({
    'LLE1': X_lle[ :,0],
    'LLE2': X_lle[ :,1],
    'LLE3': X_lle[ :,2],
    'Class': y})

# data.head()

plot = px.scatter_3d(
    data,
    x = 'LLE1',
    y = 'LLE2',
    z = 'LLE3',
    color='Class')

plot.show()

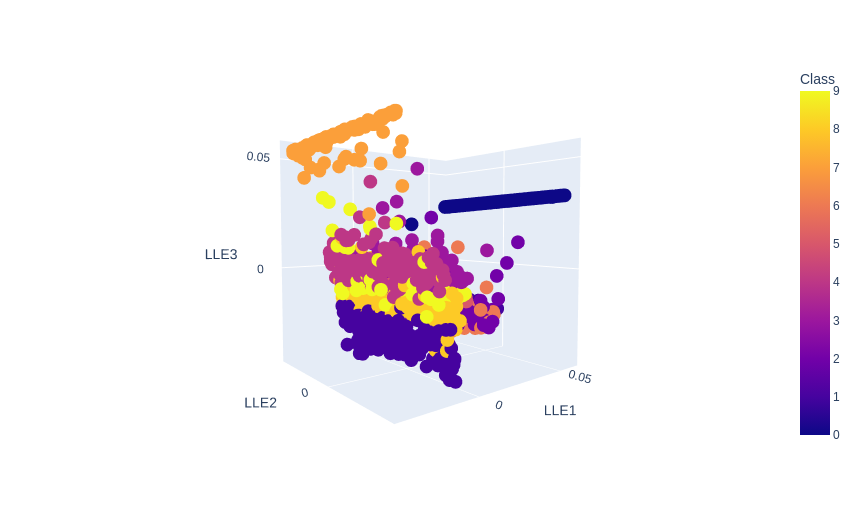
Dimensionality Reduction for Image Segmentation

no_components=3
no_neighbors=15

lle = LocallyLinearEmbedding(n_components=no_components, n_neighbors=no_neighbors)
X_lle = lle.fit_transform(X, y=y)

data = pd.DataFrame({
    'LLE1': X_lle[ :,0],
    'LLE2': X_lle[ :,1],
    'LLE3': X_lle[ :,2],
    'Class': y})

# data.head()

plot = px.scatter_3d(
    data,
    x = 'LLE1',
    y = 'LLE2',
    z = 'LLE3',
    color='Class')

plot.show()

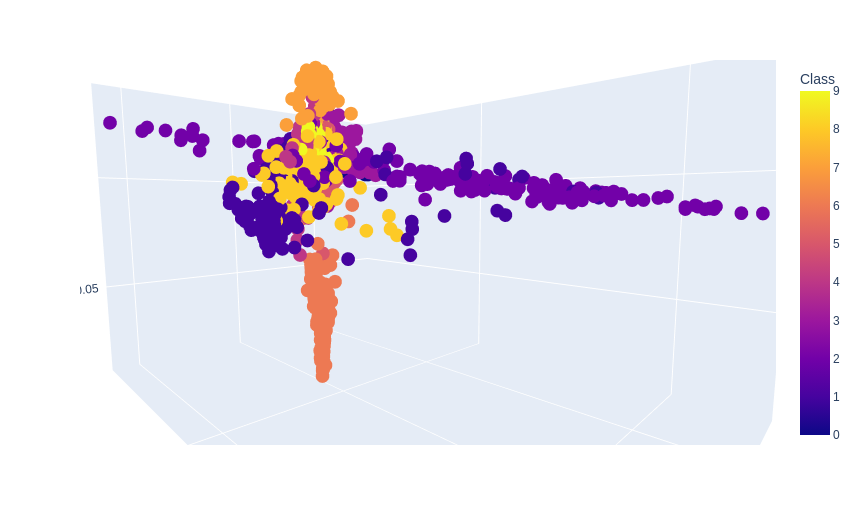
Dimensionality Reduction for Image Segmentation

no_components=3
no_neighbors=20

lle = LocallyLinearEmbedding(n_components=no_components, n_neighbors=no_neighbors)
X_lle = lle.fit_transform(X, y=y)

data = pd.DataFrame({
    'LLE1': X_lle[ :,0],
    'LLE2': X_lle[ :,1],
    'LLE3': X_lle[ :,2],
    'Class': y})

# data.head()

plot = px.scatter_3d(
    data,
    x = 'LLE1',
    y = 'LLE2',
    z = 'LLE3',
    color='Class')

plot.show()

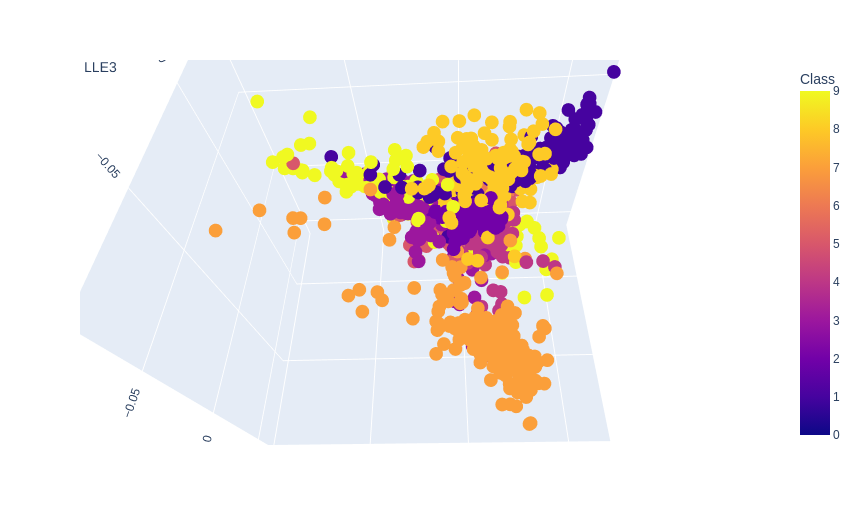
Dimensionality Reduction for Image Segmentation

Principal Component Analysis​

import matplotlib.pyplot as plt
import plotly.express as px
import pandas as pd
import seaborn as sns
from sklearn.datasets import load_digits
from sklearn.decomposition import PCA

2-Dimensional Plot​

no_components = 2
pca = PCA(n_components=no_components).fit(X)
X_pca = pca.transform(X)

data = pd.DataFrame({
    'PCA1': X_pca[:,0],
    'PCA2': X_pca[:,1],
    'Class': y})

fig = plt.figure(figsize=(10, 8))
sns.scatterplot(
    x='PCA1',
    y='PCA2',
    hue='Class',
    palette='tab10',
    data=data)

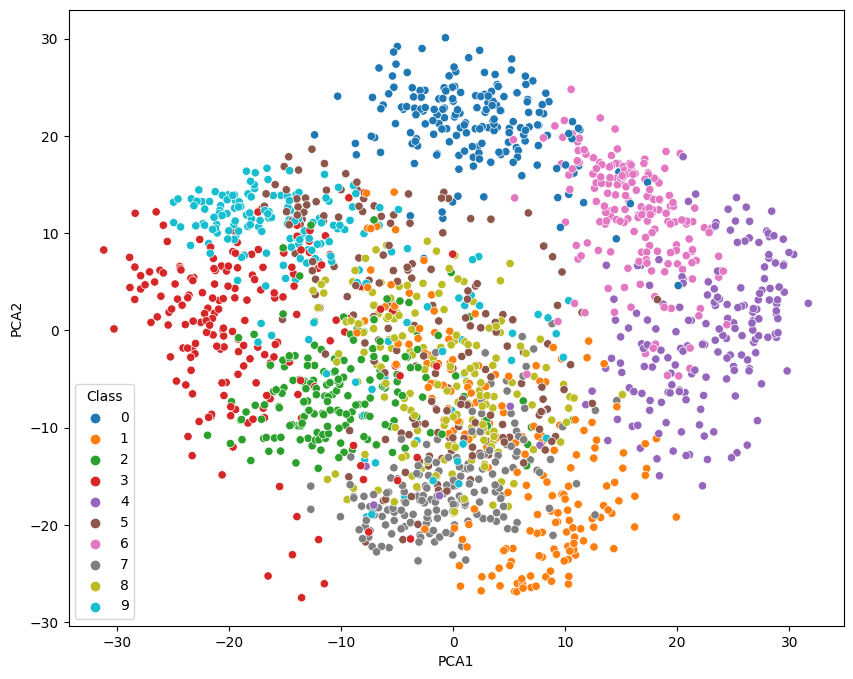
Principal Component Analysis

3-Dimensional Plot​

no_components = 3
pca = PCA(n_components=no_components).fit(X)
X_pca = pca.transform(X)

data = pd.DataFrame({
    'PCA1': X_pca[:,0],
    'PCA2': X_pca[:,1],
    'PCA3': X_pca[:,2],
    'Class': y})

plot = px.scatter_3d(
    data,
    x = 'PCA1',
    y = 'PCA2',
    z = 'PCA3',
    color='Class')

plot.show()

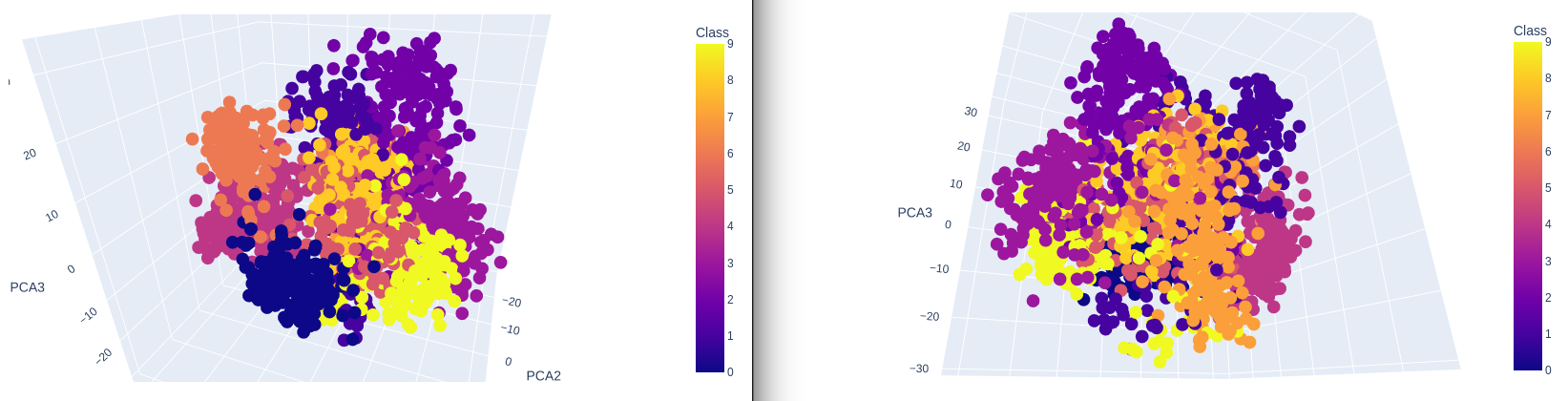
Principal Component Analysis

Fisher Discriminant Analysis​

import matplotlib.pyplot as plt
import plotly.express as px
import pandas as pd
import seaborn as sns
from sklearn.datasets import load_digits
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis

2-Dimensional Plot​

no_components = 2

lda = LinearDiscriminantAnalysis(n_components = no_components)
X_lda = lda.fit_transform(X , y=y)

data = pd.DataFrame({
    'LDA1': X_lda[:,0],
    'LDA2': X_lda[:,1],
    'Class': y})
fig = plt.figure(figsize=(10, 8))
sns.scatterplot(
    x='LDA1',
    y='LDA2',
    hue='Class',
    data=data,
    palette='tab10')

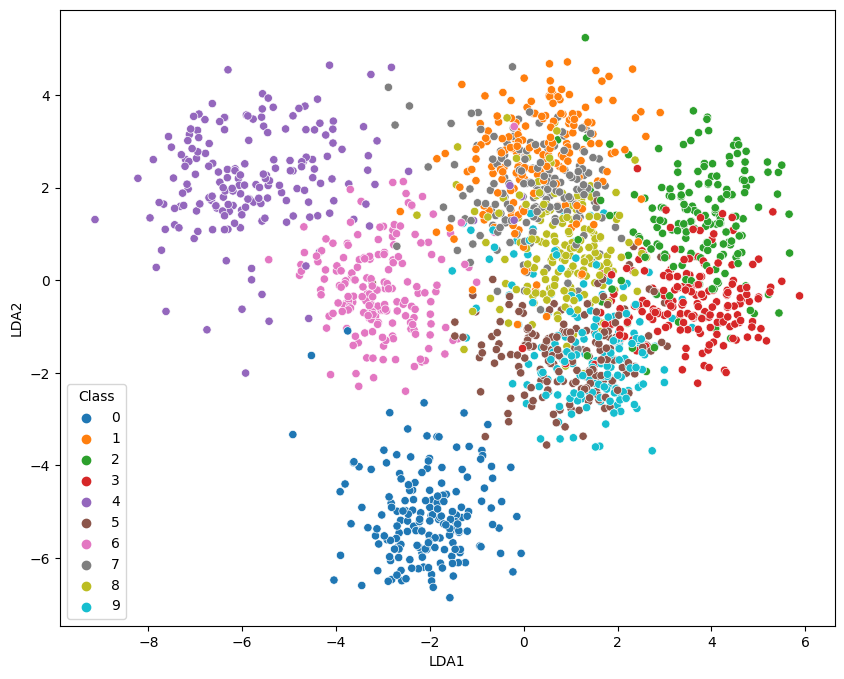
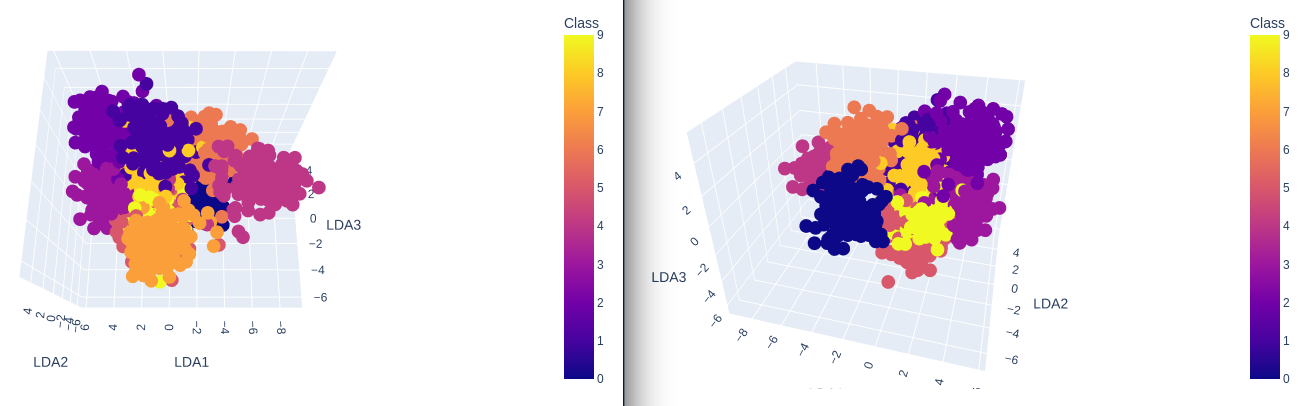
Fisher Discriminant Analysis

3-Dimensional Plot​

no_components = 3

lda = LinearDiscriminantAnalysis(n_components = no_components)
X_lda = lda.fit_transform(X , y=y)

data = pd.DataFrame({
    'LDA1': X_lda[:,0],
    'LDA2': X_lda[:,1],
    'LDA3': X_lda[:,2],
    'Class': y})

plot = px.scatter_3d(
    data,
    x = 'LDA1',
    y = 'LDA2',
    z = 'LDA3',
    color='Class')

plot.show()

Fisher Discriminant Analysis

Isometric Mapping​

import matplotlib.pyplot as plt
import plotly.express as px
import pandas as pd
import seaborn as sns
from sklearn.datasets import load_digits
from sklearn.manifold import Isomap

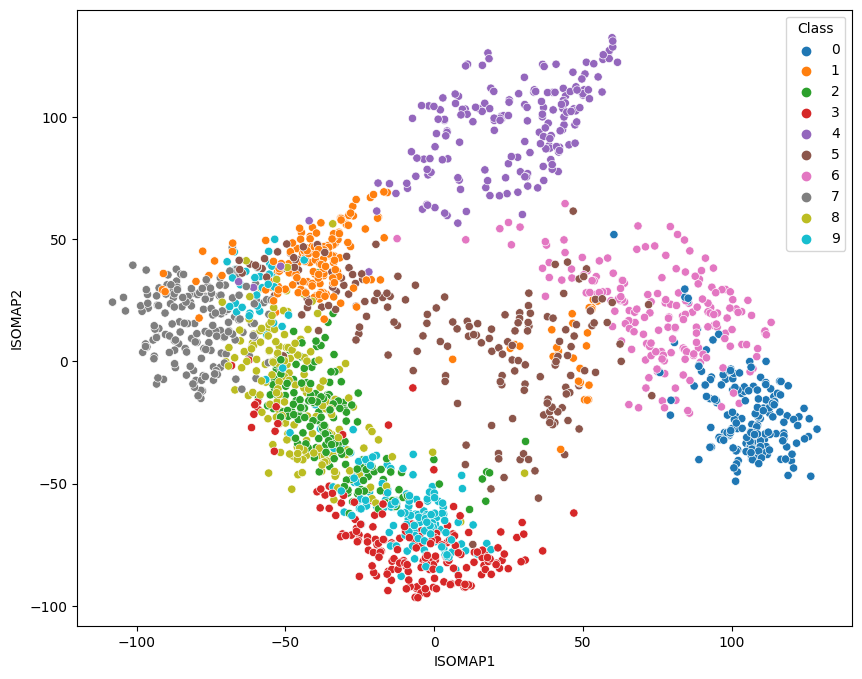
2-Dimensional Plot​

no_components = 2
k_nearest_neighbors = 10

isomap = Isomap(
    n_components=no_components,
    n_neighbors=k_nearest_neighbors)

X_iso = isomap.fit_transform(X)
print('Reconstruction Error: ', isomap.reconstruction_error())
# Reconstruction Error:  3092.669294495556

data = pd.DataFrame({
    'ISOMAP1': X_iso[:,0],
    'ISOMAP2': X_iso[:,1],
    'Class': y})
fig = plt.figure(figsize=(10, 8))
sns.scatterplot(
    x='ISOMAP1',
    y='ISOMAP2',
    hue='Class',
    data=data,
    palette='tab10')

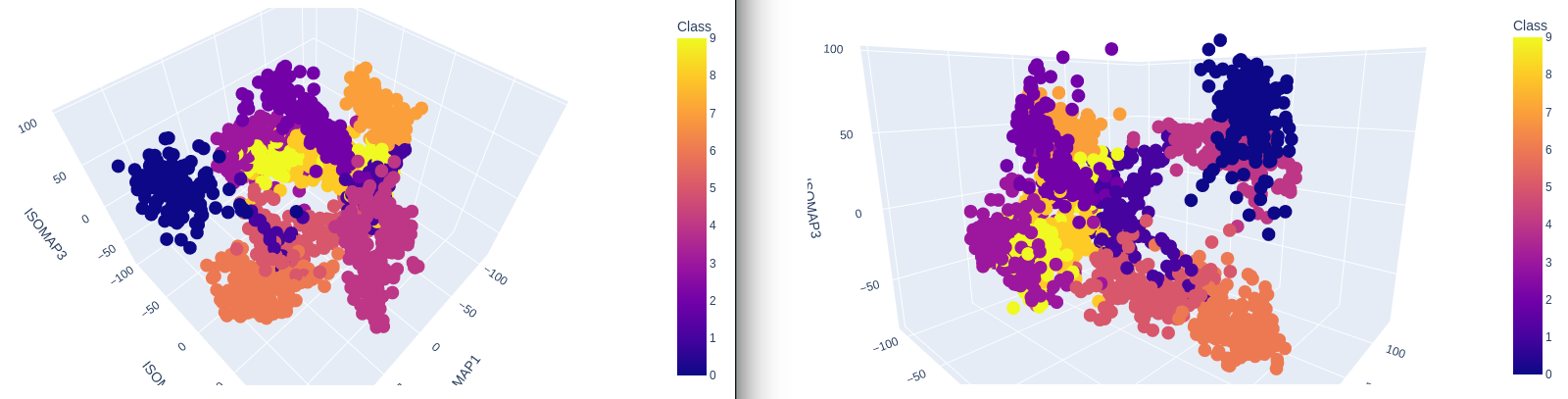
Isometric Mapping

3-Dimensional Plot​

no_components = 3
k_nearest_neighbors = 10

isomap = Isomap(
    n_components=no_components,
    n_neighbors=k_nearest_neighbors)

X_iso = isomap.fit_transform(X)
print('Reconstruction Error: ', isomap.reconstruction_error())
# Reconstruction Error:  2522.73434274533

data = pd.DataFrame({
    'ISOMAP1': X_iso[:,0],
    'ISOMAP2': X_iso[:,1],
    'ISOMAP3': X_iso[:,2],
    'Class': y})
plot = px.scatter_3d(
    data,
    x = 'ISOMAP1',
    y = 'ISOMAP2',
    z = 'ISOMAP3',
    color='Class')

plot.show()

Isometric Mapping